*Property of supplementary angles.
*Property of supplementary angles.
If α + β = 1800, then:
sinα= sinβ,cosα = -cosβ & tanα= – tanβ
*Property of complementary angles.
*Property of complementary angles.
If α + β = 900, then:
sinα = cosβ, cos α = secβ & tanα = cotβ
*The three sides and three angles are called its six elements.
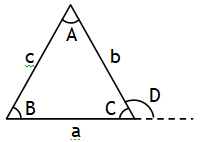
*The three sides and three angles are called its six elements. The angles are represented by the capitals letters A, B and C and the sides are represented by small letters a, b and c. Following results are useful to solve a triangle.
*Even & odd functions
*Even & odd functions
A function f (x) is called even, if f (- x) = + f (+x).
called, odd, if f (- x) = – f (+x).
otherwise called neither even nor odd.
cos and sec are even and remaining tan, cot, csc & sin are odd, thus
cos(- x) = + cos x & sec(- x) = + secx
sin(- x) = – sin x & csc(- x) = – csc x
tan(- x) = – tan x & cot(- x) = – cot x
*Transformation formulae sinA + sinB = 2sinC cosD
*Transformation formulae
sinA + sinB = 2sinC cosD
sinA – sinB = 2cosC sinD
cosA + cosB = 2cosC cosD
cosA – cosB = – 2sinC sinD
*Semi angle formulae
*Semi angle formulae
*Expansion formulae sin (A ± B) = sin A cos B ± cos A sin B
*Expansion formulae
sin (A ± B) = sin A cos B ± cos A sin B
cos (A ± B) = cos A cos B ± sin A sin B
>Trigonometric series
>Trigonometric series
*Commonly used values
*Commonly used values
*Range of T – fns sinθ & cosθ ε [ -1, +1]
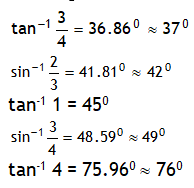
*Range of T – fns
sinθ & cosθ ε [ -1, +1]
tanθ & cotθ ε (– ∞ , +∞)
cosecθ & secθ ε (– ∞, – 1] U [+1, +∞)
