*Cramer’s rule For two simultaneous equations, a1 x + b1 y = c1 & a2 x + b2 y = c2
*Cramer’s rule
For two simultaneous equations,
a1 x + b1 y = c1 & a2 x + b2 y = c2
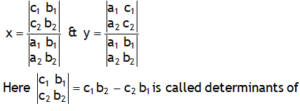
*Cramer’s rule
For two simultaneous equations,
a1 x + b1 y = c1 & a2 x + b2 y = c2
*Quadratic equation
ax2 + bx + c = 0 (a, b & c ε R with a ≠ 0)
b 2 – 4 a c = D (discriminate)
Roots of quadratic are

The following 6 situations may arise.
If D > 0, then roots are real & unequal.
If D < 0, then roots are imaginary & unequal.
If D = 0, then roots are real & equal.
If D > 0 & a perfect square, then roots are rational.
If D > 0 & not a perfect square, then roots are irrational.
If a = 1, b & c are integers, then roots are rational.
>Laws of exponents
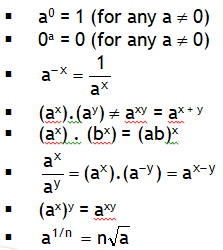
*Componendo & dividendo

*Arithmetic operations

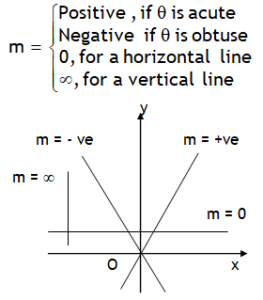
*Slope of a straight line
*Harmonic function
Functions which are periodic as well as bounded are called harmonic functions
sinθ & cosθ are harmonic.
*Bounded functions
If a function attains finite values only, then it is said to be bounded otherwise unbounded.
Only sinθ & cosθ are bounded functions, secθ, cosθ, tanθ & cotθ are unbounded.
*Periodic functions
A function is said to be periodic if it repeats itself after a fixed period. For a periodic function f (x) there exists a positive number ‘p’ such that
f (x + p) = f (x) for all x.
The smallest such value of ‘p’ is called period.
Periodicity of tan θ & cot θ is π & that of sinθ, cosθ, cscθ and secθ is 2π.
*Finding values of θ > 900
