^Work by a variable force
^Work by a variable force
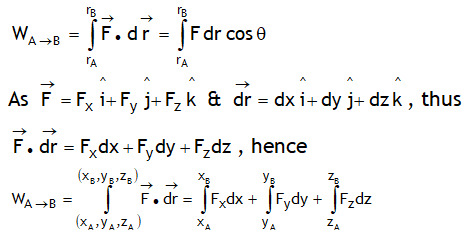
lso work = Area under F – S graph bounded with the displacement – axis.
^Work by a variable force
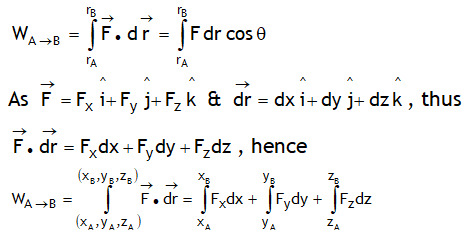
lso work = Area under F – S graph bounded with the displacement – axis.
^Work by a constant force
Work done by a constant force on a system is defined the dot product of the force acting on the system & the displacement of the system.
^Work
^Death well & Rotor
Static friction balances the weight of person & normal reaction 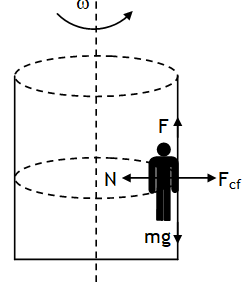
(due to centrifugal force) provides the necessary centripetal force i.e. f = mg
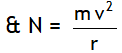
Using f = μs N, condition for

^Insect crawling in a hemisphere
Consider an insect crawling up a rough hemisphere. As the insect crawl up the force pulling it down the 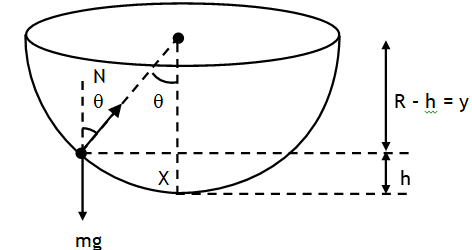
hemisphere i.e. mgsinθ increases where as normal
reaction N = mgcosθ & thus limiting friction on it decreases. Let at a height h, mgsinθ is just balanced by limiting friction.
After this height insect tends to slip back. Thus at maximum height reached by the insect.
mgsinθ = msmgsinθ or = tanθ,
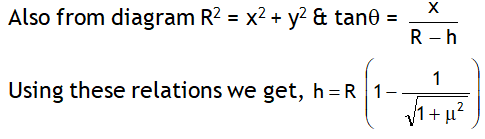
^What is cold welding
If two blocks of highly polished steel were cleaned and placed together in a perfect vacuum, they would weld themselves together and become one block of steel. This is called cold welding. In reality, small amounts of air, moisture, and contaminants accumulate on surfaces and prevent such “ideal” interactions.
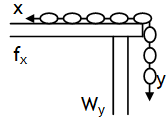
^Friction enables us to walk
In order to run or walk forward we push (P) the ground backward at some angle to vertical.
The reaction of this push can be resolved in components. 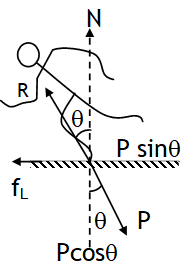
The vertical component balances our weight, where as the horizontal component push enables us to walk forward.
For no slip, FL ≥ P sinθ
or μ Pcosθ ≥ Psinθ or μ ≥ tanθ
On a smooth surface we fail to exert enough horizontal push on the ground as a result receive insufficient reaction i.e. the friction between our feet and the ground is greatly reduced, which causes us to slip. We can avoid slip by taking small steps.
^Motion on a rough inclined plane
Consider a body placed on a rough inclined plane.
The y component of the gravitational pull mg cosθ presses the plane & is balanced by normal reaction from the plane, thus N = mg cosθ.
The x component of the gravitational pull mg sinθ (say, F) tends to move the block down the plane, but can do so, only if it exceeds the limiting friction (fL = msmg cosθ) on the block.
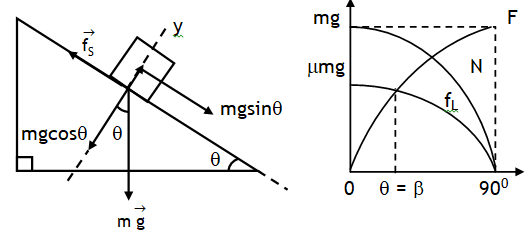
As the inclination θ is increased mgsinθ increases while the limiting frictional force (mS mg cosθ) decreases. At one stage, mgsinθ & mS mg cosθ become equal & balance each other then the body placed of the inclined plane at the verge of motion. If the block at this stage is given some velocity it will keep sliding down at constant velocity.
This angle θ is called angle of repose & abbreviated by
symbol β. At θ = β,
or mg sin θ = mS mg cosθ
or tanβ = μS
Also we can make following conclusions
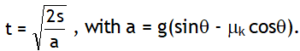 This is independent of mass of block.
This is independent of mass of block.^Chain on a rough horizontal table
Fraction of chain length that can hang without slipping on a rough table is 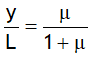
^Retardation by friction on a rough horizontal surface
An automobile is moving on a horizontal road with a speed u. If the coefficient of fiction between the tyres & the road is m. The shortest distance in which the automobile can be stopped is
